



Next: Plane Waves
Up: From the Maxwell Equations
Previous: The Maxwell Equations
Contents
In order to derive the electromagnetic wave equation in the general form, the properties of the
medium can be considered [Hecht89]. If we consider a medium we get 3 additional constitutive equations.
If the medium is a dielectric medium and is subjected to an applied electric
field, then the internal charge distribution distorts under its influence. This leads to the
generation of electric dipole moments which contribute an additional field moment. The resultant
dipole moment per unit volume is called electric polarization P. Since the field in the material
has changed, a new field quantity has to be defined, the displacement 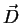
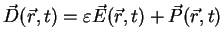 |
(A.17) |
The internal electric field 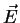 is therefore the difference between the field
is therefore the difference between the field
 ,
which would exist in absence of a polarization and the field
,
which would exist in absence of a polarization and the field
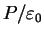 arising from the
polarization. In the same way we can define a magnetic polarization or magnetization vector
arising from the
polarization. In the same way we can define a magnetic polarization or magnetization vector 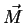 as the magnetic dipole moment per volume. In order to cover the effect of the magnetically
polarized medium a vector
as the magnetic dipole moment per volume. In order to cover the effect of the magnetically
polarized medium a vector 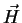 , known as the magnetic field intensity, is introduced.
, known as the magnetic field intensity, is introduced.
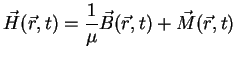 |
(A.18) |
The third constitutive equation is given by
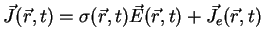 |
(A.19) |
 is the electric permittivity and
is the electric permittivity and 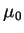 the magnetic permeability in free space.
For media other than free space the relative dielectricity
the magnetic permeability in free space.
For media other than free space the relative dielectricity
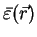 ,
the relative permeability tensor
,
the relative permeability tensor
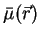 and the electric conductivity tensor
and the electric conductivity tensor
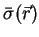 are generally dependent on the spacial location
are generally dependent on the spacial location 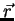 in the medium.
For homogeneous media the
in the medium.
For homogeneous media the
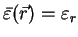 ,
,
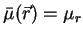 and
and
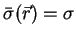 are constant for any location
are constant for any location 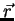 in the medium. A medium is called isotropic if
in the medium. A medium is called isotropic if
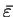 ,
,  and
and
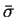 are scalar
quantities. For linear (non-ferroelectric and non-ferromagnetic) media
are scalar
quantities. For linear (non-ferroelectric and non-ferromagnetic) media
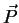 and
and 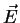 as well as
as well as 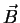 and
and 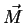 are parallel and proportional.
are parallel and proportional.
Therefore, for homogeneous, isotropic, linear media the constitutive relations can be written as
where 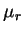 denotes the relative permeability and
denotes the relative permeability and
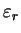 is the relative permittivity of the medium.
is the relative permittivity of the medium.
Under this conditions the Maxwell equations for linear homogeneous media can be written as
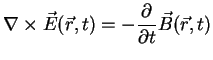 |
(A.21) |
 |
(A.22) |
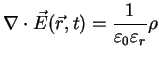 |
(A.23) |
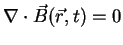 |
(A.24) |
One of the most interesting consequences arising from Maxwell 's equations is the prediction of
the existence of electromagnetic waves, long before Heinrich Rudolf Hertz (1857-1894) experimentally
proved their existence in 1887.
The general form of the wave motion equation is
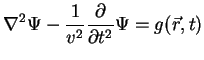 |
(A.25) |
where 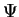 is one of the field quantities, v the propagation velocity and the disturbance
term
is one of the field quantities, v the propagation velocity and the disturbance
term
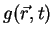 indicates the source of wave generation.
indicates the source of wave generation.
Assuming a homogeneous, isotropic, linear media we can prove, that the Maxwell equations yield
a wave equation. To achieve this, we form some second derivatives with respect to the space variables.
Taking the curl of (A.23) we obtain.
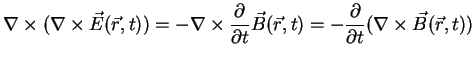 |
(A.26) |
If we now eliminate
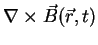 by using (A.22) the equation above becomes
by using (A.22) the equation above becomes
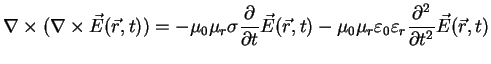 |
(A.27) |
Utilizing the operator identity (
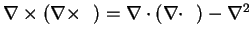 ) and, as a consequence of (A.25), that
) and, as a consequence of (A.25), that
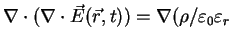 )
we find for an medium with
)
we find for an medium with
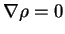
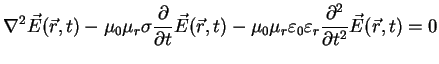 |
(A.28) |
Similarly, the corresponding result for the 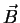 -field can be shown to be
-field can be shown to be
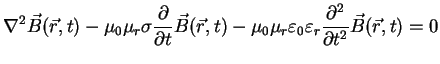 |
(A.29) |
If we assume the absence of an externally applied current we can use (A.20) to rewrite
(A.28) as
 |
(A.30) |
which shows the existence of electromagnetic waves, caused by a time varying electric current.
In nonconducting media (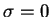 ) these equations become
) these equations become
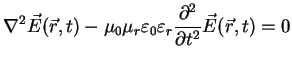 |
(A.31) |
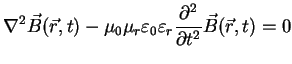 |
(A.32) |
By comparison with (A.25) it turns out that the wave propagation velocity is given by
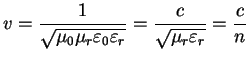 |
(A.33) |
Where
 is the propagation velocity in free space and
is the propagation velocity in free space and
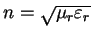 the refraction index of the medium.
the refraction index of the medium.




Next: Plane Waves
Up: From the Maxwell Equations
Previous: The Maxwell Equations
Contents