



Next: How to do a
Up: From the Maxwell Equations
Previous: Electromagnetic Waves
Contents
For remote sensing radar applications the case of time-harmonic-fields may be assumed [Kostinski86].
For time-harmonic-fields the instantaneous field vectors varies sinusoidally in time with
a single angular frequency 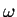
 |
(A.34) |
where  is the real part of a complex quantity,
is the real part of a complex quantity,
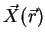 the complex field
amplitude and we choose
the complex field
amplitude and we choose 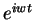 for the time dependency according to the (IEEE) convention in this treatment.
for the time dependency according to the (IEEE) convention in this treatment.
The Maxwell equations can then be simplified to
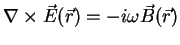 |
(A.35) |
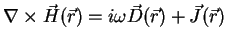 |
(A.36) |
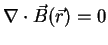 |
(A.37) |
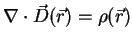 |
(A.38) |
In this case the wave equation for a source free, non conductive medium
( and
and 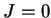 ) can be written as
) can be written as
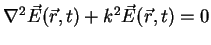 |
(A.39) |
where
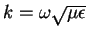 is the wave number. For plane waves we impose the
condition that, in a Cartesian coordinate system,
is the wave number. For plane waves we impose the
condition that, in a Cartesian coordinate system, 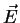 and
and 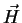 are not a function of x
and y,
if z is the propagation direction, which means that the field vector oscillates in a plane perpendicular to
the propagation direction. Such waves are called transversal electromagnetic (TEM) waves.
In this case
are not a function of x
and y,
if z is the propagation direction, which means that the field vector oscillates in a plane perpendicular to
the propagation direction. Such waves are called transversal electromagnetic (TEM) waves.
In this case
 becomes
becomes
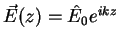 |
(A.40) |
and by applying (A.23) and (A.21) we find for the H-field
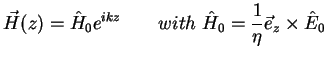 |
(A.41) |
where
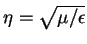 is the intrinsic impedance of the medium,
is the intrinsic impedance of the medium, 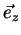 is a unit vector in propagation (z) direction and
is a unit vector in propagation (z) direction and 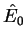 and
and 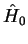 the complex amplitudes.
Similarly we find for a plane wave propagating in an arbitrary direction
the complex amplitudes.
Similarly we find for a plane wave propagating in an arbitrary direction
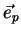
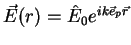 |
(A.42) |
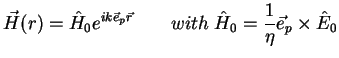 |
(A.43) |
where
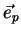 is a unit vector parallel to the propagation direction.
is a unit vector parallel to the propagation direction.
As shown above the electromagnetic wave system is made up of a set of coupled, time varying and
mutually orthogonal electric and magnetic vector fields. The field vectors are perpendicular
to the propagation direction.
For a specific time t and point in space 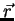 the direction and the magnitude of the
electric field vector
the direction and the magnitude of the
electric field vector
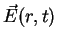 is given by the real part of the complex harmonic field expression
is given by the real part of the complex harmonic field expression
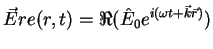 |
(A.44) |
According to Poynting's theorem, the power flux density of the wave equals the direction and
magnitude of the Poynting vector 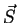
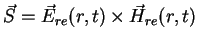 |
(A.45) |
The time average over one period
![$ t \in [0,T]$](img487.gif) of the power flux density of a harmonically varying
field is therefore given by
of the power flux density of a harmonically varying
field is therefore given by
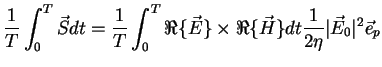 |
(A.46) |




Next: How to do a
Up: From the Maxwell Equations
Previous: Electromagnetic Waves
Contents