



Next: Polarization Synthesis
Up: Polarimetric Description of Scatterers
Previous: The Jones Matrix
Contents
Another way to describe a scatterer, which is widely used in optics is the Stokes matrix.
The Stokes vector from (2.39) may be also written as [Ulaby90]
![$\displaystyle \vec{g} = \left[ \cal R \right] \vec{G} =
\left[ \begin{array}{cc...
...ert E_v\vert^2 Vert E_h\vert^2 E_h E_v^* E_v E_h^*
\end{array} \right]$](img177.gif) |
|
|
(3.4) |
Furthermore, between the scattered vectors
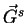 and the
transmitted vector
and the
transmitted vector
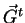 exists the following relation
[Ulaby92]
exists the following relation
[Ulaby92]
Using (2.40) and (2.41) we can now write the
Stokes vector of the scattered wave
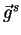 as
as
![$\displaystyle \vec{g}^{s} = \left[ \cal R \right] \vec{G}^s = \frac{1}{r^2} \le...
...\cal R \right]^{-1}\vec{g}^{t} = \frac{1}{r^2} \left[ \cal L \right]\vec{g}^{t}$](img185.gif) |
(3.6) |
where
![$ \left[ \cal R \right]^{-1}$](img186.gif) is the inverse matrix of
is the inverse matrix of
![$ \left[ \cal R \right]$](img187.gif)
![$\displaystyle \left[ \cal R \right]^{-1} =
\left[ \begin{array}{cccc}
1 & 1 & 0 & 0\\
1 & -1 & 0 & 0\\
0 & 0 & 1 & i\\
0 & 0 & 1 & -i
\end{array} \right]$](img188.gif) |
|
|
(3.7) |
![$ \left[ \cal L \right]$](img189.gif) is a
is a
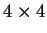 real matrix, describing the relation between the Stokes vector
of the scattered wave and the Stokes vector of the transmitted wave. This
real matrix, describing the relation between the Stokes vector
of the scattered wave and the Stokes vector of the transmitted wave. This
![$ \left[ \cal L \right]$](img189.gif) matrix is
called Stokes-matrix [Tsang95] or Müller-matrix [Jones89], [Schurcliff62].
It can be seen from the definition of the elements of
matrix is
called Stokes-matrix [Tsang95] or Müller-matrix [Jones89], [Schurcliff62].
It can be seen from the definition of the elements of
![$ \left[ \cal W \right]$](img191.gif) in (3.5), that under
the multiplication
in (3.5), that under
the multiplication
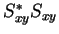 with
with 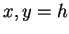 or v, the information about the absolute
phase is lost.
or v, the information about the absolute
phase is lost.
The Stokes-matrix is often used in literature [Pottier92a], [Pottier92b], [Krogager93], and mentioned here for the sake of
completeness, but will not be used further in this treatment.




Next: Polarization Synthesis
Up: Polarimetric Description of Scatterers
Previous: The Jones Matrix
Contents
![$\displaystyle \vec{g} = \left[ \cal R \right] \vec{G} =
\left[ \begin{array}{cc...
...ert E_v\vert^2 Vert E_h\vert^2 E_h E_v^* E_v E_h^*
\end{array} \right]$](img177.gif)
![]() is the inverse matrix of
is the inverse matrix of
![]()