



Next: The Stokes Matrix
Up: Polarimetric Description of Scatterers
Previous: Polarimetric Description of Scatterers
Contents
If a scatterer is illuminated by an electromagnetic plane wave transmitted by an antenna, such
that, at the scatterer the incidenct wave is given by
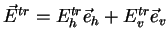 |
(3.1) |
and that induces currents in the scatterer, which in turn reradiate a scattered wave.
In the far zone of the scatterer, the scattered wave can be considered as a plane wave.
The scattering process can be modeled as a linear transformation, described by a matrix S.
The received field is then given by [Sinclair48], [Sinclair50], [Kennaugh51]
![$\displaystyle \vec{E}^{re} = \left[ S \right] \vec{E}^{tr} = \left[\begin{array...
...ray}\right] \left[\begin{array}{c} E_{h}^{tr} \\
E_{v}^{tr} \end{array}\right]$](img169.gif) |
|
|
(3.2) |
The [S]-matrix, sometimes referred to as Jones matrix [Jones41], is a complex
 matrix, containing the information about the scatterer. The elements of [S] are denoted as
the complex scattering amplitudes
matrix, containing the information about the scatterer. The elements of [S] are denoted as
the complex scattering amplitudes
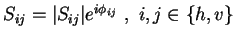 .
. 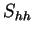 and
and 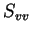 are called co-polar and
are called co-polar and
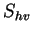 and
and 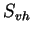 cross-polar components. Due to the reciprocity theorem for monostatic
systems and reciprocal media, the cross-polar components are equal
cross-polar components. Due to the reciprocity theorem for monostatic
systems and reciprocal media, the cross-polar components are equal
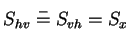 [Ulaby90].
Therefore, the [S] reduces to
[Ulaby90].
Therefore, the [S] reduces to
![$\displaystyle [S] = e^{i\phi_0} \left[\begin{array}{cc} \vert S_{hh}\vert & \ve...
...phi_x -\phi_0)} & \vert S_{vv}\vert e^{i(\phi_{vv} -\phi_0)} \end{array}\right]$](img176.gif) |
|
|
(3.3) |
Thus the [S]-matrix yields 5 independent parameters (3 amplitudes and 2 phases).




Next: The Stokes Matrix
Up: Polarimetric Description of Scatterers
Previous: Polarimetric Description of Scatterers
Contents