



Next: The Scattering Vector
Up: Polarimetric Description of Scatterers
Previous: The Stokes Matrix
Contents
The representation of the elements of the [S]-matrix are dependent on
the polarization basis. Using the results from section 4.9, we can now derive from a given
[S]-matrix in {
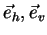 } basis, the [S]-matrix for an arbitrary
basis {
} basis, the [S]-matrix for an arbitrary
basis {
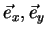 } by an unitary congruence transformation [Lüneburg96]
} by an unitary congruence transformation [Lüneburg96]
![$\displaystyle [S]_{xy}=[U]_{2 \times 2}^T [S]_{hv} [U]_{2 \times 2} \quad where...
...ho \rho^*}} \left[\begin{array}{cc} 1 & - \rho^* \rho & 1 \end{array}\right]$](img195.gif) |
(3.8) |
The scattering matrix components 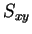 in the {
in the {
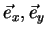 } basis, characterised by
the polarisation ratio
} basis, characterised by
the polarisation ratio  , are then given by
, are then given by
Even though the elements of [S] change under the transformation some properties of the
[S]-matrix are invariant.
- a)
- The span of the matrix, defined as the quadratic sum
of its elements, corresponds to the total power, and is constant.
- b)
- [S] is symmetric in
any arbitrary polarization bases as long as the BSA convention [IEEE79] is used, hence the reciprocity
theorem yields than that the cross-polar components are equal.
- c)
- det([S]) is invariant because
![$ det([U]_{2 \times 2}) = 1$](img165.gif) .
.
Therefore, given a [S]-matrix for an arbitrary combination of transmit and receive polarizations,
it is possible to generate the [S]-matrix for any other arbitrary combination of transmit and
receive polarizations [Boerner90]. One of the common applications of this relation is the transformation from the linear
{
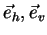 } basis to the circular {
} basis to the circular {
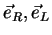 } basis. For example, for the
investigations in [Krogager95a] the cirular basis is better suited and therefore, the [S] - matrix,
measured with two linear polarized antennas
} basis. For example, for the
investigations in [Krogager95a] the cirular basis is better suited and therefore, the [S] - matrix,
measured with two linear polarized antennas ![$ [S]_{HV}$](img206.gif) is transformed in the cirular basis
is transformed in the cirular basis ![$ [S]_{RL}$](img207.gif) .
The elements of the
.
The elements of the ![$ [S]_{RL}$](img207.gif) basis for the backscatter case are given by
basis for the backscatter case are given by
If the polarization transformation properties of a target change moderately, one could envisage a radar which
dynamically adjusts the polarization in order to receive maximum power from a given target all the times [Boerner93], [Cysz91].
Such polarization tracking radars are, for instance, applied to achieve significant signal-to-clutter
enhancement and interference suppression [Poelman84].




Next: The Scattering Vector
Up: Polarimetric Description of Scatterers
Previous: The Stokes Matrix
Contents
![$\displaystyle [S]_{xy}=[U]_{2 \times 2}^T [S]_{hv} [U]_{2 \times 2} \quad where...
...ho \rho^*}} \left[\begin{array}{cc} 1 & - \rho^* \rho & 1 \end{array}\right]$](img195.gif)
![]() } basis to the circular {
} basis to the circular {
![]() } basis. For example, for the
investigations in [Krogager95a] the cirular basis is better suited and therefore, the [S] - matrix,
measured with two linear polarized antennas
} basis. For example, for the
investigations in [Krogager95a] the cirular basis is better suited and therefore, the [S] - matrix,
measured with two linear polarized antennas ![]() is transformed in the cirular basis
is transformed in the cirular basis ![]() .
The elements of the
.
The elements of the ![]() basis for the backscatter case are given by
basis for the backscatter case are given by