



Next: Non-Deterministic Scatterers
Up: Polarimetric Description of Scatterers
Previous: Polarization Synthesis
Contents
As shown in the previous section, the complex [S]-matrix describes the scattering process and
contains therefore the information about the target. Instead of the matrix notation we may use
a four-element-complex vector 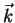 which contains the complete information
of the [S]-matrix.
which contains the complete information
of the [S]-matrix.
![$\displaystyle \left[ S \right] =\left[\begin{array}{cc} S_{HH} & S_{HV} S_{VH...
...rrow \vec{k} = \frac{1}{2} Trace([S]\Psi) = \left[ k_0, k_1, k_2, k_3 \right]^T$](img214.gif) |
(3.11) |
where
![$ Trace([S])$](img215.gif) is the sum of the diagonal elements of [S] and
is the sum of the diagonal elements of [S] and 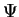 is a complete set
of
is a complete set
of
 complex basis matrices under a hermitian inner product [Cloude86b].
In principal, any complete orthonormal basis set of four
complex basis matrices under a hermitian inner product [Cloude86b].
In principal, any complete orthonormal basis set of four
 matrices can be used, as long as the
Euclidian norm of the vector
matrices can be used, as long as the
Euclidian norm of the vector 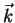 is invariant.
Two bases are widely referred in the literature. The first one, following straight forward from the
lexicographic expansion of [S] is commonly referred as Borgeaud basis [Borgeaud89]
is invariant.
Two bases are widely referred in the literature. The first one, following straight forward from the
lexicographic expansion of [S] is commonly referred as Borgeaud basis [Borgeaud89]
![$\displaystyle \Psi_B = \left\{ 2 \left[\begin{array}{cc} 1 & 0 0 & 0\end{arra...
...y} \right], 2 \left[\begin{array}{cc} 0 & 0 0 & 1\end{array} \right] \right\}$](img217.gif) |
(3.12) |
with the corresponding vector 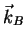 , containing the complex elements of
, containing the complex elements of ![$ [S]_{hv}$](img219.gif)
![$\displaystyle \vec{k}_B = \left[S_{hh},S_{hv},S_{vh},S_{vv}\right]^T$](img220.gif) |
(3.13) |
This vector is directly related to the system measurable.
A basis which is more related to the physics of wave scattering, commonly known as
the Pauli basis, is formed by the Pauli spin matrices [Cloude86b], [Cloude96].
![$\displaystyle \Psi_P = \left\{ \sqrt{2} \left[\begin{array}{cc} 1 & 0 0 & 1\e...
...t], \sqrt{2} \left[\begin{array}{cc} 0 & -i i & 0\end{array} \right] \right\}$](img221.gif) |
(3.14) |
As we shall see later, for the {
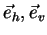 } basis the matrices represents isotropic
scattering mechanisms, (surface, dihedral,
45
} basis the matrices represents isotropic
scattering mechanisms, (surface, dihedral,
45 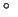 tilted dihedral, and crosspolariser). The corresponding vector
tilted dihedral, and crosspolariser). The corresponding vector  is then
is then
![$\displaystyle \vec{k}_P = \frac{1}{\sqrt{2}}\left[S_{hh}+S_{vv},S_{hh}-S_{vv},S_{hv}+S_{vh},i(S_{vh}-S_{hv}) \right]^{T}$](img224.gif) |
(3.15) |
The factor 2 in (3.12) as well as the factor 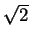 in (3.14) arises from the restriction,
that the norm of the scattering vector
in (3.14) arises from the restriction,
that the norm of the scattering vector 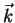 , which is equal to the total scattered power
, which is equal to the total scattered power
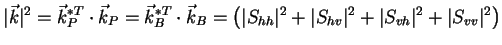 |
(3.16) |
should be independent of the choice of the basis matrices of 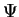 .
.
Both vectors contain the same information only in different representations.
It is, therefore, possible to transform the scattering vector 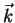 from the linear
{
from the linear
{
 }
basis into any other elliptical polarisation basis {
}
basis into any other elliptical polarisation basis {
 } [Boerner81].
} [Boerner81].
![$\displaystyle \vec{k}_{Bij}=[U]_{4B}\vec{k}_{Bhv}$](img228.gif) |
(3.17) |
The transformation basis ![$ [U]_{4B}$](img229.gif) is defined as
is defined as
![$\displaystyle [U]_{4B}= [U]_{2 \times 2} \otimes [U]_{2 \times 2}^T = \frac {1}...
... \rho & -\rho\rho^* & 1 & -\rho^* \rho^2 & \rho & \rho &1 \end{array} \right]$](img230.gif) |
(3.18) |
where  denotes the Kronecker product of matrices.
denotes the Kronecker product of matrices.
Since  is related to
is related to 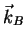 by
by
we find ![$ [U]_{4P}$](img239.gif) as
as
![$\displaystyle \left[ U_{4P}\right] = \left[ D_4 \right] \left[ U_{4B}\right]\left[ D_4 \right]^{-1}$](img240.gif) |
(3.20) |




Next: Non-Deterministic Scatterers
Up: Polarimetric Description of Scatterers
Previous: Polarization Synthesis
Contents
![$\displaystyle \left[ S \right] =\left[\begin{array}{cc} S_{HH} & S_{HV} S_{VH...
...rrow \vec{k} = \frac{1}{2} Trace([S]\Psi) = \left[ k_0, k_1, k_2, k_3 \right]^T$](img214.gif)
![]() from the linear
{
from the linear
{
![]() }
basis into any other elliptical polarisation basis {
}
basis into any other elliptical polarisation basis {
![]() } [Boerner81].
} [Boerner81].
![]() is related to
is related to ![]() by
by