



Next: Target Decomposition
Up: Polarimetric Description of Scatterers
Previous: The Scattering Vector
Contents
In the previous section we discussed deterministic scatterers which are described completely by
a single constant scattering matrix [S] or scattering vector 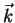 . For remote sensing
applications the assumption of pure deterministic scatterers is not valid. Since, for SAR applications,
the resolution cell is bigger than the wavelength, e.g. natural terrain surfaces contains many
spatially distributed deterministic scattering centers, each of these centers is completely
represented by an
individual
. For remote sensing
applications the assumption of pure deterministic scatterers is not valid. Since, for SAR applications,
the resolution cell is bigger than the wavelength, e.g. natural terrain surfaces contains many
spatially distributed deterministic scattering centers, each of these centers is completely
represented by an
individual ![$ [S]_i$](img241.gif) -matrix. Therefore the measured [S]-matrix for one resolution cell,
consists of the coherent superposition of the individual
-matrix. Therefore the measured [S]-matrix for one resolution cell,
consists of the coherent superposition of the individual ![$ [S]_i$](img241.gif) -matrices of all scattering
centers located within the resolution cell.
To deal with statistical scattering effects and the analysis of partial scatterers the concept
of a scatter covariance matrix or coherence matrix are introduced [Boerner81], [Cloude92], [Cloude99a], [Tragl90].
-matrices of all scattering
centers located within the resolution cell.
To deal with statistical scattering effects and the analysis of partial scatterers the concept
of a scatter covariance matrix or coherence matrix are introduced [Boerner81], [Cloude92], [Cloude99a], [Tragl90].
By forming the outer product
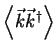 of the scattering
vectors
of the scattering
vectors 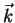 with its conjugate transposed vector
with its conjugate transposed vector
 we get a
we get a
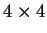 matrix. If we use the conventional scattering vector
matrix. If we use the conventional scattering vector 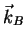 we get the so called polarimetric
covariance matrix [Boerner81],
we get the so called polarimetric
covariance matrix [Boerner81],
![$\displaystyle [C]_{4 \times 4} = \left< \vec{k}_B \vec{k}_B^\dagger \right> = \...
...S_{vv} S_{vh}^*\right> & \left< \vert S_{vv}\vert^2 \right> \end{array} \right]$](img244.gif) |
(3.21) |
where
 denotes a spatial ensemble averaging assuming homogeneity of the random scattering medium.
Analogously, the so called polarimetric coherency matrix
denotes a spatial ensemble averaging assuming homogeneity of the random scattering medium.
Analogously, the so called polarimetric coherency matrix
![$ [T]_{4 \times 4}$](img246.gif) [Cloude92] is formed as
[Cloude92] is formed as
![$\displaystyle [T]_{4 \times 4} = \left< \vec{k}_P \vec{k}_P^\dagger \right>$](img247.gif) |
(3.22) |
The polarimetric covariance/coherence matrices are of full rank (rank 4 in the four-dimensional representation).
Without the ensemble averaging both matrices have rank 1 and characterize a deterministic scattering process [Papathanassiou99].
Both matrices are by definition hermitian semi-definite matrices and have the same real non-negative eigenvalues.
but different eigenvectors.
Since the interpretation
of the physical scattering mechanisms is easier using the polarimetric coherency matrix, we will not use the polarimetric
covariance matrix further in this treatment.
However, as discussed in section 4.10, for the backscattering case the reciprocity theorem yields
 and hence, the
and hence, the 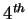 Pauli matrix (iso-cross-polarizers) can not occur.
Therefore the scattering vector from (3.15) reduces to the 3-dimensional case,
without loss of information.
Pauli matrix (iso-cross-polarizers) can not occur.
Therefore the scattering vector from (3.15) reduces to the 3-dimensional case,
without loss of information.
![$\displaystyle \vec{k}_{P3} = \frac{1}{\sqrt{2}}\left[S_{hh}+S_{vv},S_{hh}-S_{vv}, 2 S_{x}\right]^{T}$](img250.gif) |
(3.23) |
Constrained to the 3-dimensional subspace we can now use the new scattering vector
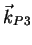 to form a
to form a
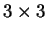 coherency matrix [T] as follows
coherency matrix [T] as follows
![$\displaystyle [T]_{3 \times 3} = \left< \vec{k}_{P3} \vec{k}_{P3}^{\dagger} \ri...
...array}{c} A=S_{hh }+S_{vv} B= S_{hh } - S_{vv} C=2S_{x}
\end{array} \right.$](img253.gif) |
|
|
(3.24) |
where
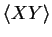 denotes a spatial ensemble averaging, assuming homogeneity of the random medium.
denotes a spatial ensemble averaging, assuming homogeneity of the random medium.
![$ {[T]}_{3 \times 3}$](img255.gif) contains the complete information on variance and correlation between all complex
elements of [S].
contains the complete information on variance and correlation between all complex
elements of [S].




Next: Target Decomposition
Up: Polarimetric Description of Scatterers
Previous: The Scattering Vector
Contents
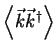 of the scattering
vectors
of the scattering
vectors 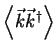 of the scattering
vectors
of the scattering
vectors ![]() with its conjugate transposed vector
with its conjugate transposed vector
![]() we get a
we get a
![]() matrix. If we use the conventional scattering vector
matrix. If we use the conventional scattering vector ![]() we get the so called polarimetric
covariance matrix [Boerner81],
we get the so called polarimetric
covariance matrix [Boerner81],
![]() and hence, the
and hence, the ![]() Pauli matrix (iso-cross-polarizers) can not occur.
Therefore the scattering vector from (3.15) reduces to the 3-dimensional case,
without loss of information.
Pauli matrix (iso-cross-polarizers) can not occur.
Therefore the scattering vector from (3.15) reduces to the 3-dimensional case,
without loss of information.