



Next: Polarimetric Description of Scatterers
Up: Wave Polarization
Previous: The Coordinate System
Contents
Subsections
Abstract - In this part we discuss how to describe a plane wave with vectors. The two common approaches are the Stokes vector representation and the Jones vector representation. For the Stokes vector representation we will show, how the representation can be visualized by means of the Poincaré sphere.
keywords: Stokes vector, Jones vector, Poincaré sphere,
In 1852 Stokes introduced a set of parameters in order to characterize the
polarization state.
The representation consists of four Stokes parameters
 and
and 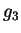 which are defined as
which are defined as
where  and
and  denotes the vertical and horizontal component (see section 4.5)
of the electric field vector
denotes the vertical and horizontal component (see section 4.5)
of the electric field vector 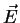 .
.
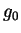 is proportional to the total intensity of the wave,
is proportional to the total intensity of the wave, 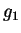 represents the
difference between the vertically and horizontally polarized intensity and expresses
the amount of linear horizontal or linear vertical polarization of the wave.
represents the
difference between the vertically and horizontally polarized intensity and expresses
the amount of linear horizontal or linear vertical polarization of the wave.
 and
and 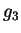 jointly represent the phase difference between the h and v component
of the electric field and can be regarded as the amount of right or left circular polarization
of the wave. [Collett93].
jointly represent the phase difference between the h and v component
of the electric field and can be regarded as the amount of right or left circular polarization
of the wave. [Collett93].
This representation is commonly referred as a Stokes vector and is valid for
completely and partially polarized waves. Even though the Stokes vector consists of 4
parameters, in the case of completely polarized waves, only three of them are independent because
the sum of the polarized components 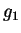 ,
, ,
,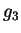 equals the total intensity of the wave.
equals the total intensity of the wave.
 |
(2.34) |
For partially polarized waves not all the intensity is contained in the polarized components and
therefore, the total intensity is bigger than the sum of the polarized components.
 |
(2.35) |
For completely polarized waves the stokes parameters can be expressed as
![$\displaystyle \vec{g} = \left[\begin{array}{c}g_0 g_0 \cos(2\psi)\cos(2\chi) \\
g_0 \sin(2\psi)\cos(2\chi) g_0 \sin(2\chi) \end{array}\right]$](img122.gif) |
|
|
(2.36) |
where 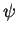 is the inclination angle from (2.18) and
is the inclination angle from (2.18) and 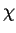 is the ellipticity angle
from (2.19).
is the ellipticity angle
from (2.19).
The state of polarization of a completely polarized plane wave can be mapped
uniquely to a point P on the surface of a sphere with radius 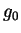 , called the
Poincaré sphere (Fig. 2.4) by regarding
, called the
Poincaré sphere (Fig. 2.4) by regarding  and
and 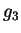 as the
Cartesian coordinates of P [Descamps51], [Descamps73], [Boerner91].
as the
Cartesian coordinates of P [Descamps51], [Descamps73], [Boerner91].
 defines the latitude and
defines the latitude and  the longitude
of P. As discussed above the sign of
the longitude
of P. As discussed above the sign of 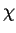 determines the handedness or orientation of the
polarization state. Therefore the upper hemisphere (
determines the handedness or orientation of the
polarization state. Therefore the upper hemisphere (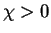 ) displays left
handed polarizations, while the lower hemisphere (
) displays left
handed polarizations, while the lower hemisphere (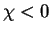 ) displays right
handed polarizations. The poles represent circular polarizations and in the
equatorial plane we find linear polarization.
) displays right
handed polarizations. The poles represent circular polarizations and in the
equatorial plane we find linear polarization.
Figure 2.4:
Poincaré sphere visualization of polarization states. linear polarization along the equator, circular polarization at the poles, elliptical polarization: the upper and lower hemisphere
|
|
As stated above (2.34) is only valid for completely polarized waves. For the
general case we have to use [Huynen87]
 |
(2.37) |
Introducing the degree of polarization p
 |
(2.38) |
the Stokes vector can be decomposed into a completely polarized and
an unpolarized component. If we define a
we can express the Stokes vector as a sum of a completely polarized and a
completely unpolarized component
This representation yields two particularly convenient features.
- a)
- the orthogonal polarization states are located on diametrically opposite points of the
Poincaré sphere.
- b)
- all four parameters can be derived from intensity
measurements, which, especially for optical applications, is a great advantage.
While the Stokes vector is still widely used for optical applications,
another representation exists and is used in this treatment. Instead of a representation
in a three-dimensional real space, a representation in a two-dimensional complex space
is preferred for radar remote sensing applications as mentioned in sections 1.3 and 1.6.
In this representation of a monochromatic plane wave, the E field is written,
as a linear combination of two arbitrary orthonormal polarization states  and
and
 weighted by their corresponding complex amplitudes
weighted by their corresponding complex amplitudes  and
and  as already stated in (2.7)
for the case of {
as already stated in (2.7)
for the case of {
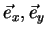 }-polarisation states.
}-polarisation states.
 |
(2.40) |
or as 2-dimensional complex vector
 as introduced by Jones [Jones41]
as introduced by Jones [Jones41]
The so called Jones vector contains the complete information about the polarization
ellipse, except the handedness, i.e. two plane waves propagating in opposite directions
have the same Jones vector representation. In order to compensate this lack of consistency
the Jones vector can be completed by using the subscripts " " and "
" and " " , where
subscript "
" , where
subscript " " denotes a wave propagating in
" denotes a wave propagating in 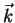 direction and subscript "
direction and subscript " "
a wave propagating in
"
a wave propagating in  direction [Lüneburg95].
direction [Lüneburg95].
 |
(2.42) |
The vectors
 are denoted as directional Jones vectors [Graves56]
where
are denoted as directional Jones vectors [Graves56]
where  is the complex conjugate of
is the complex conjugate of  and vice versa. The conjugation of
the Jones vectors is equivalent to the change of the sign of the difference angle
and vice versa. The conjugation of
the Jones vectors is equivalent to the change of the sign of the difference angle
 and thus to a change of the handedness of the polarization state.
Using the polarization ratio from (2.23) the Jones vector can also
be expressed as
and thus to a change of the handedness of the polarization state.
Using the polarization ratio from (2.23) the Jones vector can also
be expressed as
![$\displaystyle \vec{E}_{ab} = \left[\begin{array}{c} E_a E_b \end{array}\right]=
E_a \left[\begin{array}{c} 1 \rho \end{array}\right]$](img148.gif) |
|
|
(2.43) |
The polarization ratio  in (2.47) depends on the actual basis in which the
quantities are given.
In general, any orthonormal set of elliptically polarized states can form a polarization basis.
Therefore, as we change from one basis to another, also the representation of the wave changes.
If {
in (2.47) depends on the actual basis in which the
quantities are given.
In general, any orthonormal set of elliptically polarized states can form a polarization basis.
Therefore, as we change from one basis to another, also the representation of the wave changes.
If {
 } and {
} and {
 } are two orthonormal
polarisation bases, the E-field
} are two orthonormal
polarisation bases, the E-field 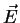 is represented as
is represented as
 |
(2.44) |
with the corresponding Jones vectors
![$\displaystyle \vec{E}_{x1,x2} = \left[\begin{array}{c} E_{x1} E_{x2} \end{ar...
...ad
\vec{E}_{y1,y2} = \left[\begin{array}{c} E_{y1} E_{y2} \end{array}\right]$](img152.gif) |
|
|
(2.45) |
The transformation of a 2-element complex vector into another is given via a
 complex matrix
complex matrix
![$ [U]_{2 \times 2}$](img154.gif) , so that
, so that
![$\displaystyle \vec{E}_{y1,y2} = [U]_{2 \times 2} \vec{E}_{x1,x2}$](img155.gif) |
(2.46) |
As a consequence of the preservation of the energy of the wave, the matrix
![$ [U]_{2 \times 2}$](img154.gif) is unitary.
With the polarization ratio
is unitary.
With the polarization ratio  of
of
 the basis vectors of the new basis {
the basis vectors of the new basis {
 } are given as [Krogager95a], [Krogager95b], [Auermann98]
} are given as [Krogager95a], [Krogager95b], [Auermann98]
![$\displaystyle \vec{e}_{y1} = e^{i\delta_{y1}} \frac{1}{\sqrt{1+\rho_{x}\rho_{x}^*}}\left[\begin{array}{c} 1
\rho_{x}
\end{array}\right]$](img158.gif) |
|
|
(2.47) |
![$\displaystyle \vec{e}_{y2} = e^{i\delta_{y2}} \frac{1}{\sqrt{1+\rho_{x}\rho_{x}^*}}\left[\begin{array}{c} - \rho_{x}^*
1 \end{array}\right]$](img159.gif) |
|
|
(2.48) |
 and
and
 represent the phase reference for the new basis states. It can be
proved, that
represent the phase reference for the new basis states. It can be
proved, that
 [Papathanassiou99].
The transformation matrix
[Papathanassiou99].
The transformation matrix
![$ [U]_{2 \times 2}$](img154.gif) is the projection of the new basis {
is the projection of the new basis {
 } onto the original basis {
} onto the original basis {
 }. This means that
the columns of the transformation matrix
}. This means that
the columns of the transformation matrix
![$ [U]_{2 \times 2}$](img154.gif) are the vectors of the new basis [Strang88]
are the vectors of the new basis [Strang88]
 and
and
 expressed in the original basis {
expressed in the original basis {
 },
with
},
with
![$ det([U]_{2 \times 2}) = 1$](img165.gif) .
.
![$\displaystyle [U]_{2 \times 2} = \frac{1}{\sqrt{1+\rho \rho^*}} \cdot
\left[\be...
...^{-i\delta_{y1}} \rho e^{i\delta_{y1}} & e^{-i\delta_{y1}}
\end{array}\right]$](img166.gif) |
|
|
(2.49) |
Where  is the polarization ratio of E in the {
is the polarization ratio of E in the {
 } basis.
The phase reference angle
} basis.
The phase reference angle
 is not important for the determination of the polarimetric parametres
of the new basis states and is usually set as
is not important for the determination of the polarimetric parametres
of the new basis states and is usually set as
 in radar polarimetry [Kong86], [Kennaugh52].
in radar polarimetry [Kong86], [Kennaugh52].




Next: Polarimetric Description of Scatterers
Up: Wave Polarization
Previous: The Coordinate System
Contents
![$\displaystyle \left[\begin{array}{c} g_0 g_1 g_2 g_3 \end{array}\right]=
...
...\\
2 E_{v0}E_{h0}\cos(\delta) 2 E_{v0}E_{h0}\sin(\delta) \end{array}\right]$](img114.gif)
![]() ,
,![]() ,
,![]() equals the total intensity of the wave.
equals the total intensity of the wave.
![]() , called the
Poincaré sphere (Fig. 2.4) by regarding
, called the
Poincaré sphere (Fig. 2.4) by regarding ![]() and
and ![]() as the
Cartesian coordinates of P [Descamps51], [Descamps73], [Boerner91].
as the
Cartesian coordinates of P [Descamps51], [Descamps73], [Boerner91].
![]() defines the latitude and
defines the latitude and ![]() the longitude
of P. As discussed above the sign of
the longitude
of P. As discussed above the sign of ![]() determines the handedness or orientation of the
polarization state. Therefore the upper hemisphere (
determines the handedness or orientation of the
polarization state. Therefore the upper hemisphere (![]() ) displays left
handed polarizations, while the lower hemisphere (
) displays left
handed polarizations, while the lower hemisphere (![]() ) displays right
handed polarizations. The poles represent circular polarizations and in the
equatorial plane we find linear polarization.
) displays right
handed polarizations. The poles represent circular polarizations and in the
equatorial plane we find linear polarization.
![\includegraphics[height=10cm]{poincare.eps}](img126.gif)
![]() is the polarization ratio of E in the {
is the polarization ratio of E in the {
![]() } basis.
The phase reference angle
} basis.
The phase reference angle
![]() is not important for the determination of the polarimetric parametres
of the new basis states and is usually set as
is not important for the determination of the polarimetric parametres
of the new basis states and is usually set as
![]() in radar polarimetry [Kong86], [Kennaugh52].
in radar polarimetry [Kong86], [Kennaugh52].