



Next: The Coordinate System
Up: Wave Polarization
Previous: Introduction
Contents
Subsections
Abstract - In this section we will introduce the description of Transversal Electro-Magnetic waves (TEM waves or just EM waves), in terms of their field vectors. In the following we will introduce the polarization ellipse and discuss some special cases of polarization and the meaning of the polarization ratio.
keywords: TEM waves, EM waves, polarization ellipse, special cases of polarization, polarization ratio
For a plane wave propagating in an arbitrary direction
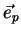 ,
the electromagnetic wave system is made up of a set of coupled, time varying and
mutually orthogonal electric and magnetic vector fields. The field vectors are perpendicular to the propagation direction (for a detailed derivation of this see Appendix A).
,
the electromagnetic wave system is made up of a set of coupled, time varying and
mutually orthogonal electric and magnetic vector fields. The field vectors are perpendicular to the propagation direction (for a detailed derivation of this see Appendix A).
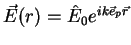 |
(2.1) |
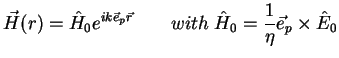 |
(2.2) |
where
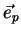 is a unit vector parallel to the propagation direction.
As we can see from the equations above, the electric field vector is directly related to the magnetic field vector and the latter can always be calculated from the electric field vector. Therefore, we will only focus on the electric fields vector in the following.
For a specific time t and point in space
is a unit vector parallel to the propagation direction.
As we can see from the equations above, the electric field vector is directly related to the magnetic field vector and the latter can always be calculated from the electric field vector. Therefore, we will only focus on the electric fields vector in the following.
For a specific time t and point in space 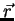 the direction and the magnitude of the
electric field vector
the direction and the magnitude of the
electric field vector
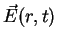 is given by the real part of the complex harmonic field expression
is given by the real part of the complex harmonic field expression
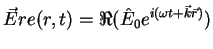 |
(2.3) |
As shown above for a transverse electro-magnetic wave, the 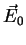 -vector oscillates in a plane
perpendicular to the propagation direction. (Fig. 2.1)
-vector oscillates in a plane
perpendicular to the propagation direction. (Fig. 2.1)
Figure:
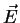 -field of a plane EM wave oscillating in a plane perpendicular to the propagation direction
-field of a plane EM wave oscillating in a plane perpendicular to the propagation direction 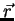
|
|
The vectorial nature of plane transverse electromagnetic
(TEM) waves is called polarization and is independent of the chosen space coordinate system.
As we shall see in the following, in the
general case, the trace of the tip of the field vector 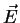 within a plane perpendicular to the propagation
direction, is an ellipse, meaning the wave is elliptically polarized. Special cases of elliptically
polarization are linear or circular polarization. Even though the polarization itself is
independent of the coordinate system, for the description of polarization a coordinate system
and a reference direction of propagation is needed. Due to the fact that the most fully
polarimetric radar systems use two orthogonal linear polarized antennas, we introduce a
Cartesian coordinate system, where z is the propagation direction. The
electric field of a wave propagating in z-direction is located in the x-y
plane and
consists of a x-component
within a plane perpendicular to the propagation
direction, is an ellipse, meaning the wave is elliptically polarized. Special cases of elliptically
polarization are linear or circular polarization. Even though the polarization itself is
independent of the coordinate system, for the description of polarization a coordinate system
and a reference direction of propagation is needed. Due to the fact that the most fully
polarimetric radar systems use two orthogonal linear polarized antennas, we introduce a
Cartesian coordinate system, where z is the propagation direction. The
electric field of a wave propagating in z-direction is located in the x-y
plane and
consists of a x-component 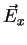 and a y-component
and a y-component 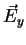 with the complex
amplitudes
with the complex
amplitudes
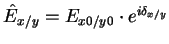
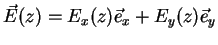 |
(2.4) |
with
 |
(2.5) |
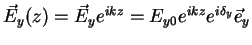 |
(2.6) |
Therefore the instantaneous values of
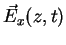 and
and
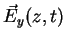 are given by
are given by
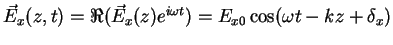 |
(2.7) |
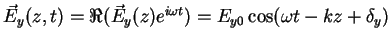 |
(2.8) |
In the general case where
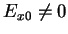 ,
,
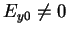 and
and
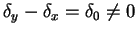 we may rewrite (2.7) and (2.8) as
we may rewrite (2.7) and (2.8) as
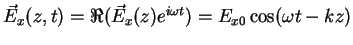 |
(2.9) |
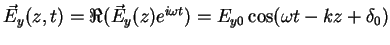 |
(2.10) |
We now eliminate the term
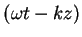 by expanding (2.7) and (2.8) into
by expanding (2.7) and (2.8) into
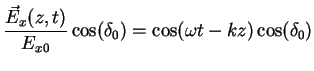 |
(2.11) |
 |
(2.12) |
we find that
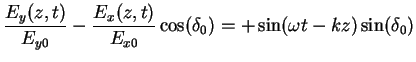 |
(2.13) |
Substituting the modified (2.12)
 |
(2.14) |
into (2.13) and rearrange the terms we get
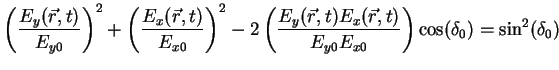 |
(2.15) |
which is the equation of an ellipse with an inclination angle 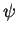 (see Fig. 2.2) such that
(see Fig. 2.2) such that
 |
(2.16) |
Figure 2.2:
Polarization ellipse in x-y-plane, rotation angle 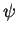 , ellipticity angle
, ellipticity angle 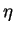 ,
and auxiliary angle
,
and auxiliary angle 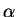 , for a wave traveling in
, for a wave traveling in 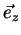 -direction (out of page)
-direction (out of page)
|
|
The polarization may also be described by the geometrical properties of the ellipse,
which are the inclination angle 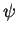 and the ellipticity angle
and the ellipticity angle 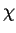
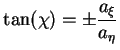 |
(2.17) |
where 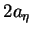 and
and 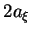 are the major and minor axes of the ellipse.
are the major and minor axes of the ellipse.
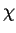 specifies the shape of the ellipse as well as the sense of rotation of the E-vector.
The polarization is left handed for
specifies the shape of the ellipse as well as the sense of rotation of the E-vector.
The polarization is left handed for 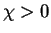 and right handed, for
and right handed, for 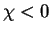 for an observer
looking in the direction of propagation.
for an observer
looking in the direction of propagation.
The polarization angles 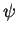 and
and 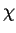 are related to the wave parameters
are related to the wave parameters
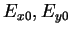 and
and
 by [Born70]
by [Born70]
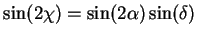 |
(2.18) |
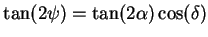 |
(2.19) |
The auxiliary angle 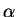 as shown in Fig. 2.2 is defined as
as shown in Fig. 2.2 is defined as
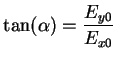 |
(2.20) |
In the previous section the polarization state was described by two parameters,
the inclination angle 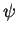 and the ellipticity angle
and the ellipticity angle 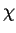 .
The same information can be expressed by a complex number, the complex polarization ratio
.
The same information can be expressed by a complex number, the complex polarization ratio  [Agrawal89],
which is the complex ratio between orthogonal components for a given basis, e.g. {
[Agrawal89],
which is the complex ratio between orthogonal components for a given basis, e.g. {
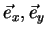 }
}
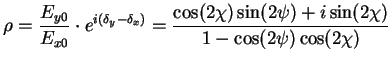 |
(2.23) |
For a given complex polarization state, we can find an orthogonal polarization state
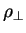 given by the orthogonality condition
given by the orthogonality condition
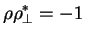 |
(2.24) |
where
 is the complex conjugate of the orthogonal polarization state of
is the complex conjugate of the orthogonal polarization state of
 [Krogager93].
These polarization states play an important role in the description of polarization as we
shall see later in this treatment.
[Krogager93].
These polarization states play an important role in the description of polarization as we
shall see later in this treatment.




Next: The Coordinate System
Up: Wave Polarization
Previous: Introduction
Contents
![]() ,
the electromagnetic wave system is made up of a set of coupled, time varying and
mutually orthogonal electric and magnetic vector fields. The field vectors are perpendicular to the propagation direction (for a detailed derivation of this see Appendix A).
,
the electromagnetic wave system is made up of a set of coupled, time varying and
mutually orthogonal electric and magnetic vector fields. The field vectors are perpendicular to the propagation direction (for a detailed derivation of this see Appendix A).
![]() within a plane perpendicular to the propagation
direction, is an ellipse, meaning the wave is elliptically polarized. Special cases of elliptically
polarization are linear or circular polarization. Even though the polarization itself is
independent of the coordinate system, for the description of polarization a coordinate system
and a reference direction of propagation is needed. Due to the fact that the most fully
polarimetric radar systems use two orthogonal linear polarized antennas, we introduce a
Cartesian coordinate system, where z is the propagation direction. The
electric field of a wave propagating in z-direction is located in the x-y
plane and
consists of a x-component
within a plane perpendicular to the propagation
direction, is an ellipse, meaning the wave is elliptically polarized. Special cases of elliptically
polarization are linear or circular polarization. Even though the polarization itself is
independent of the coordinate system, for the description of polarization a coordinate system
and a reference direction of propagation is needed. Due to the fact that the most fully
polarimetric radar systems use two orthogonal linear polarized antennas, we introduce a
Cartesian coordinate system, where z is the propagation direction. The
electric field of a wave propagating in z-direction is located in the x-y
plane and
consists of a x-component ![]() and a y-component
and a y-component ![]() with the complex
amplitudes
with the complex
amplitudes
![]()
![\includegraphics[width=15.5cm]{ellipse1.eps}](img62.gif)
![]() and
and ![]() are related to the wave parameters
are related to the wave parameters
![]() and
and
![]() by [Born70]
by [Born70]