



Next: The Vorticity Concept
Up: Target Decomposition
Previous: Context
Contents
Subsections
This type of decomposition approaches is based on the evaluation of the
scattering matrix. The basic idea behind these approaches is to express the [S]-matrix
as a complex sum of elementary scattering matrices, which can be assigned to certain deterministic
scattering mechanisms. The Pauli basis mentioned previously (3.14) , is such an approach and the
vectorization of the [S]-matrix can be interpreted as the description of a scatterer in terms
of deterministic scattering mechanisms, expressed by the Pauli matrices.
![$\displaystyle [S] = \left[\begin{array}{cc}a+b & c -id c+id & a-b \end{array}...
...\end{array} \right]+
d\left[\begin{array}{cc}0 & -i i & 0 \end{array} \right]$](img257.gif) |
|
|
(4.1) |
where a, b, c and d are proportional to the complex elements of
the scattering vector  ,
of which the
,
of which the 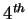 matrix is, due to the reciprocity theorem, not relevant for the
backscattering case as discussed before.
Depending on the polarization basis, physical interpretations of the basic scattering mechanisms
can be given.
Krogager, introduced a roll invariant decomposition interpretation
where the actual scattering matrix can be regarded as a superposition of the basic scattering
mechanisms isotropic surface, right wound helix and left wound helix [Krogager90].
For the case of a left wound helix,
the roll-invariant formulation can be expressed in the circular basis as follows,
matrix is, due to the reciprocity theorem, not relevant for the
backscattering case as discussed before.
Depending on the polarization basis, physical interpretations of the basic scattering mechanisms
can be given.
Krogager, introduced a roll invariant decomposition interpretation
where the actual scattering matrix can be regarded as a superposition of the basic scattering
mechanisms isotropic surface, right wound helix and left wound helix [Krogager90].
For the case of a left wound helix,
the roll-invariant formulation can be expressed in the circular basis as follows,
![$\displaystyle \left[ S \right]_{RL} =
e^{j\phi} \left\{ k_{s}e^{j\phi_s} \left[...
...{h} \left[\begin{array}{cc} e^{j2\theta} & 0 0 & 0\end{array}\right] \right\}$](img258.gif) |
|
|
(4.2) |
For the sphere, diplane, helix approach is the components are not necessarily mutually orthogonal, but yield some other advantages. Due to the roll-invariant properties and the continuous
transition of parameters in terms of invariant mechanisms, as opposed to the
orthogonal Pauli-components of which two represent the same mechanism. Thus, in
spite of the mathematical advantage and elegancy of orthogonal sets, a
practical disadvantage of the Pauli representation of polarimetric radar data
is that a double-bounce reflector shows up in two different components, one
representing an unrotated diplane, another representing a 45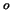 tilted
diplane. A unique advantage of the SDH representation is the property that
three different elementary scatterers (mechanisms) show up in only one out of
three components, although the diplane and helix components are not
independent (orthogonal), which means that in the presence of both a diplane
and a helix, the decomposition will in general not extract the actual strengths
of the respective reflectors.
tilted
diplane. A unique advantage of the SDH representation is the property that
three different elementary scatterers (mechanisms) show up in only one out of
three components, although the diplane and helix components are not
independent (orthogonal), which means that in the presence of both a diplane
and a helix, the decomposition will in general not extract the actual strengths
of the respective reflectors.
Decompositions of the complex scattering matrix
are particularly suited for coherent processing and cases where the
scattering is due to a few dominating scattering centers.
For the linear {
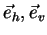 } basis, the Pauli matrices can be interpreted in a straight forward manner, as shown in Tab. 4.1
} basis, the Pauli matrices can be interpreted in a straight forward manner, as shown in Tab. 4.1
Table:
Pauli matrices and their interpretation in the {
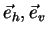 } polarisation basis
} polarisation basis
|
Pauli matrix |
scattering type |
interpretation |
![$ \left[\begin{array}{cc} 1 & 0 \newline 0 & 1 \end{array}
\right]$](img260.gif)
|
odd-bounce |
surface, sphere, cornerreflectors |
![$ \left[\begin{array}{cc} 1 & 0 \newline 0 & -1 \end{array} \right]$](img261.gif)
|
even-bounce |
dihedral |
![$ \left[\begin{array}{cc} 0 & 1 \newline 1 & 0 \end{array}
\right]$](img262.gif)
|
even-bounce  tilted tilted |
 tilted dihedral tilted dihedral |
![$ \left[\begin{array}{cc} 0 & -i\newline i & 0 \end{array}
\right]$](img264.gif)
|
cross-polariser |
not existent for backscattering |
|
|
|
|
Analogue to the Pauli decomposition, we can derive an interpretation for the Sphere/Diplane/Helix decomposition as shown in Tab. 4.2
Table:
SDH decomposition matrices and their interpretation in the {
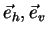 } polarisation basis
} polarisation basis
|
matrix |
scattering type |
interpretation |
![$ e^{j\phi_s} \left[\begin{array}{cc} 0 & j\newline j & 0\end{array} \right]$](img265.gif)
|
odd-bounce |
sphere, surface, cornerreflectors |
![$ \hspace{-1.2em} \left[\begin{array}{cc} e^{j2\theta} & 0\newline 0 & -e^{-j2\theta}\end{array} \right]$](img266.gif)
|
even-bounce |
(tilted) dihedral |
![$ \left[\begin{array}{cc} e^{j2\theta} & 0\newline 0 & 0\end{array}
\right] $](img267.gif)
|
helix |
helix like scattering |
|
|
|
|
Apart from the physical importance these particular mechanisms have in Radar
imagery, the Pauli decomposition has the further advantage that the scattering mechanisms
are orthogonal and so their separation is possible, even in the case of second order
statistics where noise and depolarisation
effects can be introduced.
Using the Pauli decomposition we can derive a three color composite of a fully polarimetric data set
(see Fig. 4.2) for visual classification purposes.
Figure 4.2:
RGB representation of a Pauli decomposition of an full polarimetric E-SAR data set from the test site
Oberpfaffenhofen, Germany, blue:
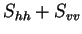 , red:
, red:
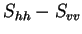 , green:
, green: 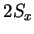
|
|
From Fig. 4.2 we can clearly distinguish structures with even-bounce characteristic (buildings),
areas with odd-bounce characteristics and finally areas where the scattering mechanism of the 3rd Pauli matrix
is dominant.
Even though this three color composite yields helpful information for the interpretation of fully polarimetric SAR data, it
is obvious that this approach is not sufficient for the interpretation of all areas in the scene. Since it is only
capable to distinguish between 3 ideal scattering mechanism and their combination some ambiguous areas remain
and a interpretation of the data is therefore difficult.
A third approach using a polar decomposition of the scattering matrix was developped by Laura Carrea at the Chemnitz University of Technology. While the afore mentioned decompositions of the [S]-matrix are additive, this approach proposes a multiplicative
decomposition of the scattering matrix. The following passage is taken from Laura's IGARSS paper [Carrea], thanks Laura ;o). As mentioned before the decomositions described above are performed as a sort of sum of more
elementary quantities. An alternative idea is to consider a
multiplicative decomposition which could be useful in order to try
to reduce the coherent speckle noise which is multiplicative. In
the coherent case, such a decomposition could be the polar
decomposition of the scattering matrix.
The polar decomposition is based on a mathematical theorem
[Fano] asserting that any non-singular operator is uniquely
expressible in the form (the polar form):
 |
(4.3) |
where H is a Hermitian operator and U is a unitary one, such that:
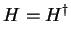 (definite) (definite)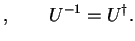 |
(4.4) |
Choosing a basis, operators are represented by numbers. The
scattering matrix is the representation of the S operator, for
example, in HV basis:
![$\displaystyle S=\left[ \begin{array}{cc} S_{HH} & S_{HV} S_{VH} & S_{VV} \end{array}\right],$](img272.gif) |
(4.5) |
where the S elements are complex numbers. It is always possible to
"normalize" the S matrix, finding a matrix 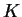 such that:
such that:
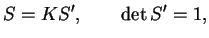 |
(4.6) |
where:
![$\displaystyle K=\left[ \begin{array}{cc} \sqrt{\det S} & 0 0 & \sqrt{\det S} \end{array}\right].$](img275.gif) |
(4.7) |
The scattering matrix (4.3) becomes:
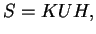 |
(4.8) |
where
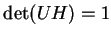 . The Hermitian and the unitary matrices, in
such a decomposition, result:
. The Hermitian and the unitary matrices, in
such a decomposition, result:
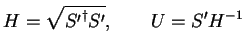 |
(4.9) |
The elements of the two matrices are in function of the scattering
matrix components.
The scattering mechanism can be interpreted as two particular
kinds of transformations on the input wave: a boost 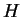 and a
rotation
and a
rotation  . The action of such transformations is independent of
the basis that is chosen to represent the operators, because
. The action of such transformations is independent of
the basis that is chosen to represent the operators, because 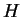 and
and  are still Hermitian and unitary whatever representation
has been chosen.
are still Hermitian and unitary whatever representation
has been chosen.
Consequently, a peculiarity of such a decomposition is its
independence of the polarization basis. As a result, the action of
the transformation can be geometrically represented.
To have an idea about the action of a boost transformation, a pure
boost [Rindler] in the z direction is considered. The boost
transforms the polarization and the intensity of the wave. The
visualization of the action of the boost on a polarization is
realized on the Poincaré sphere. The point P moves on the
Poincaré sphere along the direction of the boost, z in this
case, due to the increment in the module of the boost parameter
(Fig. 4.3). A boost is always a transformation along a
specific direction.
The visualization of the action of the boost on the intensity
could be performed in a three dimensional space, because we have
been dealing only with monochromatic waves. For such waves in the
four dimensional Stokes space, the relation
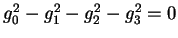 holds;
holds; 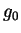 ,
, 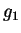 ,
,  ,
, 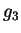 are the Stokes parameters. Neglecting all the points in which
are the Stokes parameters. Neglecting all the points in which
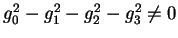 holds, we can collect all the
points such that
holds, we can collect all the
points such that
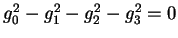 and build a three
dimensional space with them.
and build a three
dimensional space with them.
Figure 4.3:
The effect of a boost on the Poincaré sphere.
|
|
In such a space the action of a
particular boost on all the points of the Poincaré sphere is
shown in Fig. 4.4.
Figure 4.4:
The visualization of a boost for completely polarized waves.
|
|
All the points coming out from the transformation build an
ellipsoid up, and the polarization, laying on the direction of the
axis of the boost, corresponds to the maximum intensity.
A unitary transformation can be visualized on the Poincaré
sphere, because it doesn't influence the intensity of the wave. It
results in a transformation around a direction, as shown in
Fig. 4.5, for the z direction.
Figure 4.5:
The effect of a rotation on the Poincaré sphere.
|
|
To any rotation is associated a quantity ("spin matrix" or
"rotation operator") [Misner]:
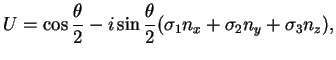 |
(4.10) |
where 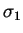 ,
, 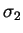 ,
,  are the Pauli matrices.
Writing explicitly the Pauli matrices, the U matrix results:
are the Pauli matrices.
Writing explicitly the Pauli matrices, the U matrix results:
![$\displaystyle U = \left[ \begin{array}{cc} \cos\frac{\theta}{2}-in_{x}\sin\frac...
...ta}{2} & \cos\frac{\theta}{2}+in_{x}\sin\frac{\theta}{2} \end{array}\right],$](img290.gif) |
(4.11) |
where 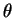 is the angle of rotation and
is the angle of rotation and
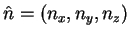 is the axis of rotation.
is the axis of rotation.
In the same way, it is possible to associate a quantity to any
boost, which results:
![$\displaystyle H = \left[ \begin{array}{cc} \cosh\frac{\alpha}{2}+m_{x}\sinh\fra...
...a}{2} & \cosh\frac{\alpha}{2}-m_{x}\sinh\frac{\alpha}{2} \end{array}\right],$](img293.gif) |
(4.12) |
where 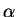 is the so called "boost rapidity" and
is the so called "boost rapidity" and
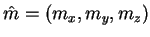 is the axis of the boost. Consequently,
the scattering matrix, expressed in (4.8), is now expressed
in function of 8 independent parameters:
is the axis of the boost. Consequently,
the scattering matrix, expressed in (4.8), is now expressed
in function of 8 independent parameters:  ,
,  , the
boost parameters,
, the
boost parameters, 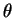 ,
,  , the rotation parameters,
, the rotation parameters,
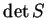 .
.
The discussion is now restricted to a very important case for
polarimetric radar, in which monostatic measurements predominate.
If the target and the propagation medium have reciprocal
constitutive relations, the reciprocity theorem holds. The
consequence of it is that the scattering matrix is symmetric:
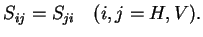 |
(4.13) |
The symmetry creates a limitation on the parameters and not all
the possible boosts and rotations are allowed. The imposition of
the reciprocity condition on the scattering matrix, as a function
of the boost and rotation parameters and of 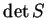 , gives:
, gives:
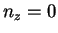 |
(4.14) |
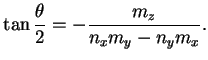 |
(4.15) |
The first condition (4.14) is on the rotation axis:
the rotation axis must lay on the 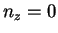 plane. The second one
(4.15) is a relation between boost and rotation
parameters.
plane. The second one
(4.15) is a relation between boost and rotation
parameters.
It is necessary to make a choice: we choose to let the boost free
and we impose both the symmetry conditions on the unitary matrix.
It will be the unitary matrix which will force the symmetry. In
such a case, the rotation angle given by (4.15) will
produce always a rotation as shown in Fig. 4.6.
Figure 4.6:
Rotation satisfying the reciprocity condition
|
|
The rotated vector has the third component in opposition to the
starting vector.
As stated before, the axis of the boost corresponds to the maximum
intensity. So, if the reciprocity theorem holds, and we send the
polarization correspondent to the axis of the boost, we receive
the polarization (canonical polarization) correspondent to the
maximum intensity. In fact, the rotation under the reciprocity
conditions moves the axis of the boost to the mirrored one respect
to the 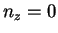 plane (equatorial plane). After the imposition of
the symmetry condition, only 5 independent parameters are left:
plane (equatorial plane). After the imposition of
the symmetry condition, only 5 independent parameters are left:
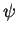 and
and 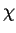 , the spherical coordinates of the unit
vector
, the spherical coordinates of the unit
vector 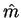 ,
,
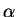 , the boost rapidity,
, the boost rapidity,
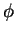 , the polar coordinate of the unit vector
, the polar coordinate of the unit vector
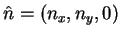 ,
,
- k, the modulo of
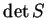 .
.




Next: The Vorticity Concept
Up: Target Decomposition
Previous: Context
Contents
![$\displaystyle [S] = \left[\begin{array}{cc}a+b & c -id c+id & a-b \end{array}...
...\end{array} \right]+
d\left[\begin{array}{cc}0 & -i i & 0 \end{array} \right]$](img257.gif)
![]() } basis, the Pauli matrices can be interpreted in a straight forward manner, as shown in Tab. 4.1
} basis, the Pauli matrices can be interpreted in a straight forward manner, as shown in Tab. 4.1
![\includegraphics[width=15cm]{decompoverview.eps}](pauli_op.gif)
![]() and a
rotation
and a
rotation ![]() . The action of such transformations is independent of
the basis that is chosen to represent the operators, because
. The action of such transformations is independent of
the basis that is chosen to represent the operators, because ![]() and
and ![]() are still Hermitian and unitary whatever representation
has been chosen.
are still Hermitian and unitary whatever representation
has been chosen.
![]() holds;
holds; ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the Stokes parameters. Neglecting all the points in which
are the Stokes parameters. Neglecting all the points in which
![]() holds, we can collect all the
points such that
holds, we can collect all the
points such that
![]() and build a three
dimensional space with them.
and build a three
dimensional space with them.
![]() plane (equatorial plane). After the imposition of
the symmetry condition, only 5 independent parameters are left:
plane (equatorial plane). After the imposition of
the symmetry condition, only 5 independent parameters are left: