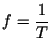 |
(1) |
Martin Hellmann
paddy@gmx.co.uk
For mechanical waves we need a medium for the wave to propagate. If we consider a rope fixed at one end a few feet above the ground and held by you at the other end as such a medium, a wave can be created by vertically shaking the end of the rope. By shaking the the end of the rope only once a single vibration is produced. This is a pulse. By moving a rope regularly up and down, a traveling or periodic wave is produced.
If we move the rope regularly up and
down, any point on a transverse wave (i.e. on the rope) moves up and down in a
repeating pattern. The shortest time that a point takes to return to the
initial position (one vibration) is called period, T. The number of
vibrations per second is called frequency ( f) and is measured in
Hertz (Hz). The equation for frequency is therefore, given by:
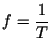 |
(1) |
![\includegraphics [width=14cm]{wave.eps}](img3.gif)
|
| (2) |
The velocity of a wave can be defined in many different ways, focusing on different aspects or components of any given wave. For example, in a wave packet (consisting of a collection of waves) each wave moves with a phase velocity, while whole wave packet moves with a group velocity, which can be different from the phase velocity. This effect is called dispersion and shall not be discussed here in more detail. In this treatment we will only consider the group velocity of the wave packet, which corresponds to the classical particle velocity.
An other important feature of a wave is the amplitude A.
The amplitude A can have slightly different meanings depending upon the context of the situation. The most general definition is, that the amplitude is the displacement of the medium from its undisturbed position to the top of a crest. In some publications it is referred as the maximum positive displacement of the medium from its undisturbed position to the top of a crest. In other discussions, though, the term amplitude takes on a slightly more complicated meaning. In some contexts, amplitude means the displacement of the medium from its undisturbed position to its disturbed position at a certain point along the wave. The definition of amplitude of a wave as the distance from a crest to where the wave is at equilibrium, is used to measure the energy transferred by the wave. The bigger the distance (i.e. the amplitude), the greater the energy transferred. While in discussions about interference, amplitude usually means the displacement of the medium from its normal position at certain points, and this displacement can be positive or negative.
In general, waves may have any shape, e.g. saw tooth like oscillations. However, in the case of SAR sine and cosine functions (called harmonic functions) are used to create the waveform. Oscillations which can be described by a single term of the sine or cosine function are called simple harmonic oscillations ( SHO). Simple harmonic oscillation can be represented as the projection of uniform circular motion onto one axis Fig. 2
The phase angleThe process of energy transport is, in general similar for electromagnetic waves and mechanical transverse waves. A wave is generated by an oscillating source (in case of the rope mentioned above, the oscillating source is the hand moving up and down) Due to the coupling of the elements of the media the each element forces it's neighbor to start the same oscillation with a time delay. In this way the wave propagates through the medium. If we observe one element of the wave we find, that each element of the wave oscillates around its undisturbed position. During this oscillation process the for each element of the wave an exchange between two energy forms takes place. In case of the rope the each element changes between potential energy and kinetic energy. Each element of the rope changes continously from potential energy and kinetic energy. E.g when the element is at the maximum distance from the undisturbed position it has the maximum potential energy and no kinetic energy (at the turning point the speed of the element is zero) on the way down it accelerates and gains kinetic energy until it gets the maximum speed (i.e. kinetic energy) at crossing the undisturbed position where the potential energy is zero.
In this case the wave is not created by a hand moving a rope up and down like in the mechanical case described above. Instead, the wave is created by moving charged particles in an antenna creating a so called electric force field. In physics, a force field is a way to picture the effects that electric charges have on one another. We can say a charge creates a force "field" in the empty space around it. a second charge with the same sign (++) put down at any place in this force field is pushed away, a charge with opposite sign (+-) set down at the same place is pulled towards. One can visualize "lines" of force by looking at the forces created by the field in many different places; imagine connecting the lines from all the electrons you have placed. The lines in such a pattern are known as "lines of force." One may imagine those lines as the connection between the elements like the rope in the mechanical case. Moving one charge causes the field lines attached to it to wiggle, and after a time the other charge starts to wiggle. Therefore, the wave here consists of a wiggling line of electric force which you can think of as being "attached" to the vibrating charge. In case of an antenna a great number of electrons are moving. As a result loops of electric lines of force are formed which move away from the charges along rays (Fig. 4).
In case of the electromagnetic wave the two energy forms which are
exchanged are not potential and kinetic energy, but electric and magnetic
fields. It can be shown (see Appendix Maxwell equations) that these fields are
coupled and form together the electromagnetic wave. Since the the electrical
and magnetic field of an electromagnetic wave are coupled (see Appendix Maxwell
equations) the wave can be described entirely be the electromagnetic field
vector ![]() .
.
Polarization is a property of a wave. The probably most commonly know application are polarizing filters which are used in photography and in certain kinds of sunglasses. But polarization is also used in digital watches and laptop screens. For example, at a beach you can use polarizing sunglasses to reduce reflected glare off of the surface of the water. If the lens is vertical, all of the sunlight reflected off from the water comes through. If the lens is horizontal, none of the reflected light comes through. To explain this we go a step back and try to explain polarization in the case of a mechanical wave. Therefore, we use the again the example of the rope.
As mentioned above each element of the wave oscillates in a plane perpendicular to the propagation direction of the wave. This means, if we define a Cartesian coordinate system with the rope (i.e. the propagation direction) as z-direction an the axis horizontal to the ground as y- direction and the vertical axis as x-axis) each element of the rope oscillates in the x-y-plane while the wave propagates in z-direction. (for a more detailed explanation about the coordinate system and the standard convention see Appendix Coordinate system). If we move our hand (the source up and down all elements of the wave oscillates in a straight line along the x-axis, or if we move the hand left and right all elements of the wave oscillates in a straight line along the y-axis. If we project the trace of an element in a plane perpendicular to the propagation direction, the trace forms a straight line. The wave is linear polarized. If we move the hand in a circle, or more general elliptical the projection of the trace of an element in a plane perpendicular to the propagation direction forms a circle or an ellipse, the wave is circularly or elliptically polarized.
Analog, in the case of an
electromagnetic wave, the projection of the tip the field vector ![]() . The
electric force field in any plane of the wave can be separated into a vertical
and horizontal component, so one can think of a diagonal oscillation of the
elements as being made up of some vertical polarized oscillation and some
horizontal polarized oscillation. If the components have a phase shift we get a
elliptically polarized wave. Electric forces in one plane of polarization are
completely equivalent to the electric forces in a vertical plane plus the
forces in a horizontal plane. Therefore, by measuring two orthogonal components
(e.g. the horizontal and the vertical component we can measure or send every
possible polarization state of the wave. You might want to try the applet below.
. The
electric force field in any plane of the wave can be separated into a vertical
and horizontal component, so one can think of a diagonal oscillation of the
elements as being made up of some vertical polarized oscillation and some
horizontal polarized oscillation. If the components have a phase shift we get a
elliptically polarized wave. Electric forces in one plane of polarization are
completely equivalent to the electric forces in a vertical plane plus the
forces in a horizontal plane. Therefore, by measuring two orthogonal components
(e.g. the horizontal and the vertical component we can measure or send every
possible polarization state of the wave. You might want to try the applet below.
Java Applet
Two waves with plains orthogonal to each other can be used to create polarized light.
If you use this Applet frequently
or if you are having ideas for further Applets, please send me an email. Thank you!
As mentioned above electromagnetic waves are produced by vibrating electric charges. For our purposes, it is sufficient to merely say that an electromagnetic wave is a transverse wave which has both an electric and a magnetic component. If you could view an electromagnetic wave traveling towards you, then you would observe the vibrations of the wave occurring in more than one plane of vibration. This is quite different than what you might notice if you were to look along a longitudinal wave (e.g. a s sound wave or a wave along a coil) and observe the wave traveling towards you. Indeed, the coil would be vibrating back and forth rather than up and sown as in the case of a transverse wave; yet these vibrations would occur in a single plane of space. Unlike the longitudinal wave, the electric and magnetic vibrations of an electromagnetic wave occur in numerous planes. E.g. An EM wave which is vibrating in more than one plane is referred to as being unpolarized. For example, light emitted by the sun is unpolarized light. Such light waves are created by electric charge which vibrates in a variety of directions, thus creating an electromagnetic wave which vibrates in a variety of directions. This concept of unpolarized waves is rather difficult to visualize. In general, it is helpful to picture unpolarized waves as a wave which is composed of many polarized waves with different poalrizations.
It is possible to transform an unpolarized wave into a polarized wave. Polarized waves are waves in which the vibrations occur in a single plane (or only in one circular sense of rotation, if you have circular polarized waves). The process of transforming unpolarized waves into polarized waves is known as polarization. There are a variety of methods of polarizing light.
A common example for this kind of filters are Polaroid filters, which are able to polarize light because of the chemical composition of the filter material. The filter can be thought of as having long-chain molecules that are aligned within the filter in the same direction. During the fabrication of the filter, the long-chain molecules are stretched across the filter so that each molecule is (as much as possible) aligned in say the vertical direction. As unpolarized light strikes the filter, the portion of the waves vibrating in the vertical direction are absorbed by the filter. The general rule is that the electromagnetic vibrations which are in a direction parallel to the alignment of the molecules are absorbed.
The alignment of these molecules gives the filter a polarization axis. This polarization axis extends across the length of the filter and only allows vibrations of the electromagnetic wave that are parallel to the axis to pass through. Any vibrations which are perpendicular to the polarization axis are blocked by the filter. Thus, a Polaroid filter with its long-chain molecules aligned horizontally will have a polarization axis aligned vertically. Such a filter will block all horizontal vibrations and allow the vertical vibrations to be transmitted (see Fig. 5). On the other hand, a Polaroid filter with its long-chain molecules aligned vertically will have a polarization axis aligned horizontally; this filter will block all vertical vibrations and allow the horizontal vibrations to be transmitted. The same principle is used for polarization filters in sun glasses. The filter does not distort the shape or dimensions of the object; it merely serves to produce a dimmer image of the object since one-half of the light is blocked as it passed through the object. If you apply two filters with perpendicular orientation all the light from an object is blocked and the object can no longer be seen. This can be also visualized by a picket-fence analogy for the mechanical tranverse wave (rope) mentioned above. A picket fence can act as a polarizer by transforming an unpolarized wave in a rope into a wave which vibrates in a single plane. The spaces between the pickets of the fence will allow vibrations which are parallel to the spacings to pass through while blocking any vibrations which are perpendicular to the spacings. Obviously, a vertical vibration would not have the room to make it through a horizontal spacing. If two picket fences, positioned behind each other, are oriented in such a way that the pickets are both aligned vertically, then vertical vibrations will pass through both fences. If the pickets of the second fence are aligned horizontally, then the vertical vibrations which pass through the first fence will be blocked by the second fence. For electromagnetic waves the same principle applies. Instead of the filters we use now linear polarized antennas. If we transmit a wave with a vertical dipole the wave is vertically polarized. If we use a second dipole for receiving the wave we can see the same effect. If the dipoles are oriented parallel (e.g. both vertical) the wave will cause the electrons in the receiving dipole to oscillate, resulting into a current in the dipole which we can measure. In that case we can receive the signal transmitted from the first dipole. If the dipoles are oriented perpendicular the dipoles are de-coupled) and no signal can be received. In any other case, the receiving dipole will only measure the projection of the incoming wave onto the axis of the receiving dipole.
Unpolarized waves can also undergo polarization by reflection off of surfaces. The extent to which polarization occurs is dependent upon the angle at which the wave approaches the surface and upon the material which the surface is made of. For oblique incidence angles the reflection of a wave is dependent on the polarization of the wave in relation to the orientation of the surface. For example, unpolarized light can undergo polarization by reflection off of water surfaces. The extent to which polarization occurs is dependent upon the angle at which the light approaches the surface and upon the material which the surface is made of. Water surfaces reflect light such that there is a large concentration of vibrations in a plane parallel to the reflecting surface. A person viewing objects by means of light reflected off of the water surfaces will often perceive a glare if the extent of polarization is large. Light reflected off a lake is partially polarized in a direction parallel to the water's surface. The use of glare-reducing (polarized) sunglasses with the proper polarization axis allows for the blocking of this partially polarized light. By blocking the plane-polarized light, the glare is reduced.
Polarization or depolarization can also occur when a wave is
scattered while traveling through a medium. The polarization axis of a wave can
change due to reflections. For example a 45![]() tilted diplane will change a
horizontally polarized wave into a vertically polarized one and vice versa. If
a linear polarized radar wave travels through a volume (e.g. a forest) the wave
is scattered often and the reflected wave will be depolarized. Especially the
change of polarization due to scattering is used for polarimetric radar remote
sensing. The polarization properties of the transmitted wave are affected by
the scattering occurring on the ground. By measuring the reflected wave and
comparing it to the transmitted wave, one can make conclusions about the
scattering process on the ground. This will be discussed in more detail in the
advanced polarimetry tutorial.
tilted diplane will change a
horizontally polarized wave into a vertically polarized one and vice versa. If
a linear polarized radar wave travels through a volume (e.g. a forest) the wave
is scattered often and the reflected wave will be depolarized. Especially the
change of polarization due to scattering is used for polarimetric radar remote
sensing. The polarization properties of the transmitted wave are affected by
the scattering occurring on the ground. By measuring the reflected wave and
comparing it to the transmitted wave, one can make conclusions about the
scattering process on the ground. This will be discussed in more detail in the
advanced polarimetry tutorial.